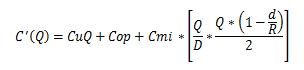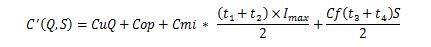INVENTARIOS
¿QUÉ SON LOS INVENTARIOS?
¿QUÉ SON LOS INVENTARIOS?
Inventarios son bienes tangibles que se tienen para la venta en el curso ordinario del negocio o para ser consumidos en la producción de bienes o servicio para su posterior comercialización. Los inventarios comprenden, además de las materias primas,productos en proceso y productos terminados o mercancías para la venta, el inventario también incluye lo que la empresa utiliza para mantener el negocio en marcha y funcionando, por ejemplo, el almacenamiento de los limpiadores se considera inventario para un negocio que se centra en el negocio de la limpieza.
¿POR QUÉ EXISTEN?
La razón fundamental es por que resulta físicamente imposible y económicamente poco práctico el que cada artículo llegue al sitio donde se necesita y exactamente cuando se necesita, puesto que no existe una respuesta instantánea por parte de los proveedores, y aún cuando a un proveedor le sea físicamente posible suministrar materias primas con intervalos de unas cuantas horas, por ejemplo, esto será prohibitivo debido al costo involucrado.
GESTIÓN DEL INVENTARIO
Independientemente de la forma de inventario que tenga una empresa, la gestión inadecuada de ese inventario puede dar lugar a excesos en el pedido de materiales, y la pérdida del mismo. La mala gestión de inventario en un almacén o en una empresa puede incluso resultar en el robo: elementos de almacenamiento pueden ser robado sin el conocimiento de la empresa, si el inventario no está bien rastreados.
La baja de las existencias de inventario puede dar lugar a consumidores descontentos o pobre tiempo de producción. Imagine una empresa que no dispone de todas las piezas que necesita para complementar los pedidos en el momento oportuno. Además imaginar una empresa que tiene que pausar la producción para esperar que las de partes que faltan lleguen a su almacén, no puede realizar mucho trabajo y quienes ordenaron el producto pueden estar completamente insatisfechos con la empresa del servicio. Ahora imagina una empresa que anuncia determinados productos a la venta y no tiene suficiente de las existencias para satisfacer la demanda de los clientes, una vez más, los clientes insatisfechos y descontentos son el resultado.
La gestión de inventario puede darse en alguno de estos tres modos:
- La logística del aprovisionamiento: se ocupa del proceso de adquisición y almacenamiento de productos que pueden ser materias primas, materiales, partes, piezas, etc.
- La logística de operaciones: se encarga del movimiento y almacenamiento de materiales, componentes y producto intermedios a lo largo del proceso productivo.
- La logística de distribución: Se encarga del transporte, comercialización y venta
MODELOS DE INVENTARIO
1. MODELO EOQ sin faltante
(Economic order quantity)
Este modelo tiene como base el mantener un inventario sin falta de productos para desarrollar las actividades de cualquier empresa, es decir, una empresa que maneje este modelo de inventario no se puede quedar sin mercancías para la venta.
MODELOS DE INVENTARIO
1. MODELO EOQ sin faltante
(Economic order quantity)
Este modelo tiene como base el mantener un inventario sin falta de productos para desarrollar las actividades de cualquier empresa, es decir, una empresa que maneje este modelo de inventario no se puede quedar sin mercancías para la venta.
Supuestos:
-Demanda constante y conocida.
- No se admiten faltantes.
- Existe un costo de mantener en inventario cmi
- Existe un costo de pedir Cp
- Los costos no sufren fluctuaciones por el cambio del dolar.
- La reposición es instantánea.
-Demanda constante y conocida.
- No se admiten faltantes.
- Existe un costo de mantener en inventario cmi
- Existe un costo de pedir Cp
- Los costos no sufren fluctuaciones por el cambio del dolar.
- La reposición es instantánea.
Representación gráfica del modelo
El inventario máximo y la cantidad económica pedida se representan iguales para este modelo, y el costo total para un periodo en este modelo esta conformado por tres componentes de costo: Costo unitario del producto , Costo de ordenar una compra y Costo de mantener un producto en almacén.
Cabe anotar que la expresión :
Es el área sombreada en la figura.Luego para conocer la ecuación de costo total se multiplica en ambos lados por N, y se obtiene:
Se tienen además las siguientes relaciones:

Y reemplazándolas en la ecuación 1) obtenemos:
La ecuación 2) representa el costo total anual, ahora bien se procederá a calcular la cantidad óptima a ordenar, Q óptimo:

y despejando Q se encuentra que :
Cuando se ordena esta cantidad se incurre en un costo mínimo y cualquier otra cantidad pedida ocasiona un costo mayor.
El objetivo de este modelo es encontrar la cantidad óptima que minimiza el costo total, y si representamos gráficamente los componentes del costo total se puede apreciar el punto óptimo:
2. MODELO EOQ con faltantes
Es normal que ocurran pequeños faltantes cuando por ahorrar dinero en el tiempo de preparación se pida un lote que no alcance para cubrir todo el ciclo. Sin embargo también existirá un costo asociado a los faltantes, que llevará a que estos no sean excesivos.
Supuestos:
-Demanda constante y conocida.
- Se admiten faltantes.
- El costo del faltante por una unidad de demanda insatisfecha por unidad de tiempo es Cf
- Existe un costo de mantener en inventario Cmi
- Existe un costo de pedir Cp
- Los costos no sufren fluctuaciones por el cambio del dolar.
- La reposición es instantánea.
Representación gráfica del modelo
Podemos ver en la gráfica que los niveles de inventarios de extienden a valores negativos que reflejan el numero de unidades del producto que faltaron o que están pendientes. Además podemos extraer de ella algunas relaciones que necesitaremos mas adelante:
Puede observarse que :
sustituyendo I max por (Q-S) y despejando t1 se obtiene:
Por relación de triángulos nuevamente: ( Notese que t= Q/D)
Para calcular el costo total del período se deben incluir el costo de pedido, el costo de adquisición, el costo de mantener inventario y además, el costo por faltantes (Cf) en función de Q y S, donde S es la cantidad faltante.
Ahora necesitaremos las relaciones encontradas anteriormente, reemplazandolas en la ecuación 1) y multiplicando a ambos lados de la igualdad por N=D/Q pata obtener el costo total anual resulta:
Igualando a 0 y despejando S y Q de las ecuaciones 3) y 4) respectivamente se obtiene:
y finalmente reemplazando 5) en 6)
o lo que es lo mismo:
3. MODELO LEP sin faltantes
(Lote económico de producción)
Es frecuente que los artículos sean producidos internamente en lugar de ser adquiridos a un proveedor externo. En dichos casos, el supuesto de que todos los artículos llegan juntos una vez ordenados es falsa y se recurre a un modelo con producción a tasa constante.
Al igual que en el modelo EOQ estándar, se supondrá que la demanda es deterministica y ocurre a tasa constante. También se supondrá que no se admite escasez. El modelo supone que los productos son fabricados a una tasa R constante de unidades por unidad de tiempo, luego durante un intervalo de tiempo de longitud t se producen exactamente p*t uidades
Sea:
d: demanda por unidad de tiempo
R: la tasa de producción
Cmi: costo de mantener una unidad en inventario
Cop: Costo de prender la máquina
Cu: costo producir por unidad
D: demanda anual por el producto
Asumiendo que la producción comienza en el instante 0, la variación en el tiempo del nivel de inventario se muestra en la siguiente figura:
Representación gráfica del modelo
Cuando comienza el periodo existe una producción a tasa constante R. Suponiendo que R> d ( para poder satisfacer la demanda), el inventario crece a una tasa de R-d artículos por unidad de tiempo. Luego el nivel máximo de inventario se puede calcular como t1(R-d).
Del gráfico se encuentran las siguientes relaciones:
y se conoce además que
Para calcular el costo total del período se deben incluir el costo de prender la máquina, el costo de producción y el costo de mantener inventario, en función de Q.
El costo promedio mantener en inventario por ciclo corresponde al área encerrada en el triangulo de lados d, (r-d) y (t1+t2) y es:
Teniendo en cuenta lo anterior el costo total para un periodo obedece a la expresión:
Ahora bien reemplacemos las relaciones encontradas de la gráfica en la ecuación 1)
y multiplicando a ambos lados de la igualdad por N=D/Q y haciendo las respectivas simplificaciones para obtener el costo total anual resulta:
Y finalmente derivamos la función 3)con respecto a Q para encontrar su valor óptimo para el cual se obtiene un costo mínimo :
4. MODELO LEP con faltantes
Este modelo de inventario sugiere que se la empresa lleve a cabo operaciones hasta llegar a un nivel máximo de producción (Inventario máximo, después de esto se dispone a detener la producción hasta agotar las existencias, y luego que esto suceda deben volver a empezar el proceso de producción. pero a diferencia del anterior se admiten faltantes.
Las variables a tener en cuenta son:
t1= timepo que transcurre desde que se inician operaciones hasta que se alcanza el Inventario máximo
t2= tiempo que transcurre en agotra el inventario máximo
t3= tiempo en el que acumulan los pedidos pendientes
t4=tiempo transcurrido entre cuando se vuelve a empezar operaciones hasta que el sistema se nivela con los pedidos pendientes
S= pedidos pendientes
Cu= costo unitario
Cop= costo de operación
Cmi= cosot de mantener en inventario
Cf= costo causado por las faltantes
Del gráfico se observan las siguientes relaciones:
El costo total para un periodo obedece a la expresión:
y reemplazando las relaciones encontradas anteriormente en esta ecuación se obtiene:
Y posteriormente para hallar el costo total anual se procederá a multplicar ambos lados de la igualdad por N ( recuerdese que N= D/Q)

Finalmente se calcula S y Q óptimos mediante las técnicas de derivación aplicadas en los otros modelos como sigue:
Reemplazando esta expresión en 10) se obtiene:
De ahí que:
Y reemplazando este valor en la ecuación 10:
4. MODELO EOQ con descuento por cantidad
Este modelo consiste en manejar diferentes costos de acuerdo a la cantidad de productos a comprar , es decir el número de unidades que se compren definirá el precio de los mismas. En este caso, la variable critica de decisión es el costo unitario, ya que el costo de pedir y el costo de mantener en inventario permanecen constantes sin importar la cantidad a pedir.
El modelo EOQ con des-cuentos por cantidad es una extensión del modelo básico de EOQ revisado anteriormente y mantiene sus supuestos. Se asume que el costo de adquisición (C) disminuye en la medida que aumenta el tamaño de lote. Adicionalmente se considera que el costo de almacenar una unidad en inventario es un porcentaje (I) del costo de adquisición. Por tanto la fórmula a utilizar es:
Al existir un descuento por cantidad o volumen de compra se genera un incentivo a pedir lotes de un mayor tamaño, sin embargo, esto a la vez incrementa el costo de mantener unidades en inventario. Por tanto se busca determinar la cantidad óptima a pedir para cada nivel o quiebre de precios, analizar si dicho tamaño de pedido es factible, ajustar el tamaño de lote si es necesario y finalmente comparar las distintas alternativas para ver cuál de ellas provee el menor Costo Total
El siguiente ejemplo ilustrará perfectamente de lo que se ha hablado:
EJEMPLO: Una empresa ofrece a sus clientes una serie de descuentos por volumen de
compras, dicho descuento se muestra en la siguiente tabla.
¿Qué cantidad debe ordenarse para minimizar los costos totales?
Datos suministrados:
Cp= 49$/prod.
Cmi= 20% de Cu
Solución:
El primer lugar deberán hallarse las cantidades óptimas para cada costo unitario:
Como 700 unidades esta dentro del rango, se presumirá que esta es la cantidad óptima
En este caso, 711 no se encuentra dentro del rango, es inferior, por lo cual se asumirá como cantidad óptima para este descuento 1000 unidades que es el menor número de unidades que aplican para este descuento.
Nuevamente el valor encontrado es inferior a los valores que puede tomar para el descuento en cuestión y se asumirá entonces que la cantidad óptima es 2500.
Ahora se procederá a calcular los costos totales anuales para cada cantidad:
:
Puede concluirse entonces que la cantidad óptima a pedir es de 1000 unidades ya que se incurre en el menor costo total anual
5. MODELO EOQ con demanda probabilística
Los anteriores modelos asumen que la demanda es determinística, sin embargo en la realidad eso no se presenta. El siguiente modelo tiene en cuenta este hecho y se expondrá a continuación.
Se contempla los mismos supuestos que el modelo EOQ sin faltante, por lo cual sus ecuaciones son las mismas. Ahora se considera que la demanda cumple una distribución normal, con una media X-trazo y una desviación S.
En la siguiente gráfica es una distribución normal centrada en la demanda promedio del tiempo de entrega dL donde d es la demanda diaria promedio y L es el tiempo de entrega.
En la siguiente gráfica es una distribución normal centrada en la demanda promedio del tiempo de entrega dL donde d es la demanda diaria promedio y L es el tiempo de entrega.
Como se observa, si se pide siempre la misma cantidad, en un 50% de las veces, la demanda superará nuestro inventario, y en el 50% restante, nuestro inventario estará por encima de la demanda.
Como casi siempre una posibilidad del 50% de quedar sin existencias es muy alto, se debe agregar un inventario de seguridad,el cual esta basado en el nivel de servicio o nivel de confianza, que es la probabilidad de tener un artículo en almacén cuando se necesite. Existirá entonces un porcentaje permitido de las veces en las que la demanda será mayor que nuestras existencias que se llamará alfa.
Una vez que se escoge el nivel de servicio, la cantidad de inventario de seguridad que se necesita se
encuentra como se muestra en la figura siguiente.
Una vez que se escoge el nivel de servicio, la cantidad de inventario de seguridad que se necesita se
encuentra como se muestra en la figura siguiente.
El efecto del inventario de seguridad se muestra en la siguiente figura
El punto de reorden se incrementa para proporcionar mayor protección contra los faltantes durante el
tiempo o período de entrega , entonces la fórmula para el punto de reorden ( R ) es:
Es necesario además establecer un punto de reorden, siendo este la mínima cantidad de unidades permitidas en el inventario. Apenas se llegue a este valor, es necesario montar un nuevo pedido, y de este modo se estará anticipando a la demanda.
tiempo o período de entrega , entonces la fórmula para el punto de reorden ( R ) es:
EJERCICIO:
Se tienen los datos:
Dado el nivel de servicio del 95%, Con ayuda de las tablas de normalidad se encuentra el Z correspondiente a este valor:
Se tienen los datos:
Se conoce además que la demanda es en promedio semanalmente de 154 focos con una desviación de 25. Y que la empresa maneja una política donde se tiene un nivel de servicio del 95%. Encuentre ahora el punto de reorden bajo dicha política.
Solución:
Dado el nivel de servicio del 95%, Con ayuda de las tablas de normalidad se encuentra el Z correspondiente a este valor:
Procedemos ahora a calcular el punto de reorden:
Investigación de operaciones, Taha, Hamdy. A